Gerak Lurus Tak Beraturan (Pengertian, Ciri, dan Contoh)
GERAK LURUS TAK BERATURAN
Gerak Lurus Berubah Beraturan
Jika benda yang bergerak mengalami perubahan kecepatan dan perubahan kecepatannya itu besarnya tetap, maka benda tersebut dikatakan melakukan gerak lurus berubah beraturan. Jika kecepatannya semakin cepat berarti benda tersebut mengalami percepatan. Sedangkan jika kecepatannya makin lambat dikatakan mengalami perlambatan. Untuk benda yang mengalami perlambatan biasanya diberi tanda negatif. Agar dapat dikatakan gerak lurus berubah beraturan maka percepatan dan perlambatan ini besarnya harus bersifat tetap atau konstan. Secara grafis dapat kita gambarkan sebagai berikut.
Jika suatu benda bergerak mengalami percepatan, maka akan terjadi perubahan kecepatan pada benda tersebut. Besarnya kecepatan akhir benda yang mengalami percepatan atau perlambatan dapat rumuskan sebagai berikut.
V = Vo + a.t
dimana:
V adalah kecepatan akhir benda setelah mengalami percepatan atau perlambatan dalam m/s
Vo adalah kecepatan awal atau mula-mula.
a adalah percepatan atau perlambatan yang dialami benda.
t adalah waktu yang dihabiskan.
Jika kita gambarkan dalam bentuk grafik maka hubungan antara perubahan kecepatan dengan perubahan waktu dapat dilihat pada gambar berikut.
V = Vo + a.t
dimana:
V adalah kecepatan akhir benda setelah mengalami percepatan atau perlambatan dalam m/s
Vo adalah kecepatan awal atau mula-mula.
a adalah percepatan atau perlambatan yang dialami benda.
t adalah waktu yang dihabiskan.
Jika kita gambarkan dalam bentuk grafik maka hubungan antara perubahan kecepatan dengan perubahan waktu dapat dilihat pada gambar berikut.
Sedangkan persamaan lintasan yang ditempuh oleh benda yang mengalami percepatan atau perlambatan dapat dirumuskan sebagai berikut.
Secara grafis hubungan antara jarak yang ditempuh dengan perubahan waktu dapat digambarkan sebagai berikut.
Ciri-ciri Gerak Lurus Berubah Beraturan (GLBB)
- Kecepatan berubah secara teratur (tiap detik menempuh jarak yang tidak sama).
- Percepatan konstan/tetap (ada pertambahan kecepatan tiap satuan waktu).
Contoh Gerak Lurus Berubah Beraturan (GLBB)
Contoh benda yang melakukan Gerak lurus berubah beraturan (GLBB) :
- Benda jatuh bebas. Benda jatuh bebas dari ketinggian tertentu, semakin lama kecepatannya semakin besar.
- Naik sepeda tanpa di kayuh pada jalan yang menurun. Sepeda akan bergerak semakin lama semakin cepat.
- Naik mobil pada jalan lurus dengan menginjak pedal gas secara teratur. Gerak mobil semakin lama semakin cepat.
Misalnya, sebuah benda yang dijatuhkan dari ketinggian tertentu, kecepatannya sedikit demi sedikit akan berubah menjadi suatu nilai tertentu yang semakin lama akan semakin cepat atau semakin lambat. Gerak semacam ini disebut gerak lurus berubah beraturan.
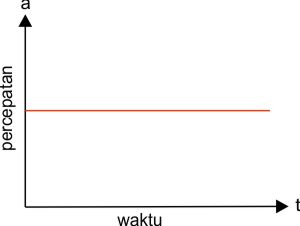
Grafik Percepatan terhadap Waktu
Grafik hubungan percepatan dengan waktu adalah seperti garis horisontal yang sejajar dengan sumbu x. Mau di detik berapun percepatan yang dialamai oleh beda yang melakukan GLBB adalah tetap. Berikut gambar grafiknya
Grafik Kecepatan terhadap Waktu
Bentuk grafik hubungan antara kecepatan dan waktu adalah seperti persamaan garis lurus. Grafik tersebut memiliki kemiringan (gradien) tertentu. Coba sobat amati grafik di atas. Grafik hubungan V dan t jika kecepatan awal(Vo) adalah nol ditunjukkan oleh grafik a dan jika kecepatannya adalah Vo maka grafiknya seperti tampak pada grafik b.
Grafik Kecepatan terhadap Waktu
Bentuk grafik hubungan antara kecepatan dan waktu adalah seperti persamaan garis lurus. Grafik tersebut memiliki kemiringan (gradien) tertentu. Coba sobat amati grafik di atas. Grafik hubungan V dan t jika kecepatan awal(Vo) adalah nol ditunjukkan oleh grafik a dan jika kecepatannya adalah Vo maka grafiknya seperti tampak pada grafik b.

Dari grafik di atas bisa sobat amati adanya kemiringan (gradien garis). Pada prinsipnya rumus kecepatan pada GLBB Vt = Vo + at sama seperti rumus pada persamaan garis lurus y = mx + c. Vt dianalogikan dengan y, c dianalogikan dengan kecepatan awal Vo, dan mx dianalogikan dengan at. Besarnya percepatan a akan sama dengan kemiringan garis (gradien). Rumusnya
a = tan θ
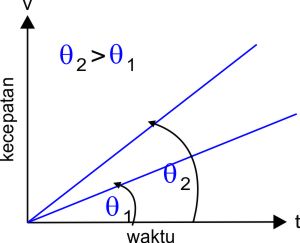
Jadi, pada gerak lurus berubah beraturan kemiringan grafik hubungan v dengan t adalah sama dengan percepatan yang terjadi pada gerak tersebut. Semakin curam grafik tersebut maka semakin besar percepatannya. Dengan melihat ilustrasi di bawah ini sobat bisa tahu bahwa grafik a yang lebih curam punya percepatan yang lebih besar dari grafik b yang bentuknya lebih landai.
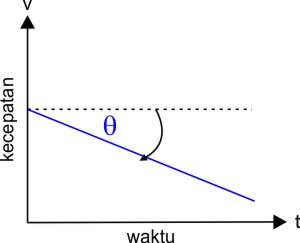
Untuk grafik hubungan v dan t yang bergerak dari kiri bawah ke kanan atas maka nilai percepatannya adalah positif yang berarti GLBB dipercepat. Akan tetapi ada juga grafik hubungan v dan t yang bergerak dari kiri atas ke kanan bawah, yaitu untuk GLBB diperlambat dengan nilai percepatan negatif. Simak grafiknya berikut
Dari grafik di atas bisa sobat amati adanya kemiringan (gradien garis). Pada prinsipnya rumus kecepatan pada GLBB Vt = Vo + at sama seperti rumus pada persamaan garis lurus y = mx + c. Vt dianalogikan dengan y, c dianalogikan dengan kecepatan awal Vo, dan mx dianalogikan dengan at. Besarnya percepatan a akan sama dengan kemiringan garis (gradien). Rumusnya
a = tan θ
Jadi, pada gerak lurus berubah beraturan kemiringan grafik hubungan v dengan t adalah sama dengan percepatan yang terjadi pada gerak tersebut. Semakin curam grafik tersebut maka semakin besar percepatannya. Dengan melihat ilustrasi di bawah ini sobat bisa tahu bahwa grafik a yang lebih curam punya percepatan yang lebih besar dari grafik b yang bentuknya lebih landai.
Untuk grafik hubungan v dan t yang bergerak dari kiri bawah ke kanan atas maka nilai percepatannya adalah positif yang berarti GLBB dipercepat. Akan tetapi ada juga grafik hubungan v dan t yang bergerak dari kiri atas ke kanan bawah, yaitu untuk GLBB diperlambat dengan nilai percepatan negatif. Simak grafiknya berikut
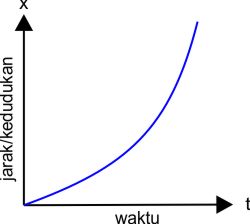
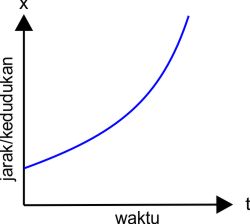
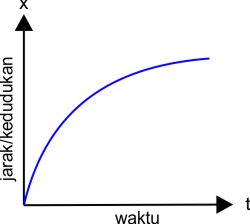
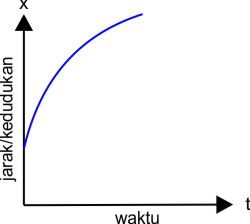
Grafik Hubungan Jarak(kedudukan) dengan Waktu :
Grafik terakhir dalam GLBB adalah hubungan antara jarak atau kedudukan terhadap waktu. Saat kita belajar GLBB kita tahu persamaan untuk mencari jarak adalah
x = xo + vot + 1/2at2
Jika sobat lihat dari persamaan di atas jaraka (x) adalah fungsi kuadrat dari waktu (t). Seperti yang kita pelajari tentan fungsi kuadrat, grafik fungsi kuadrat berbentuk parabola. Berikut kemungkinan grafik hubungan x dengan t pada gerak lurus berubah beraturan.
Sumber : http://www.uniksharianja.com/2015/06/gerak-lurus-beraturan-glb-dan-gerak-lurus-berubah-beraturan-glbb.html http://lifeontherefrigerator.blogspot.co.id/2014/11/gerak-lurus-berubah-beraturan-glbb.html http://rumushitung.com/2014/04/07/grafik-gerak-lurus-berubah-beraturan-glbb/






Komentar
Posting Komentar